En image si tu le sais pas encore, permet moi de te le dire :
Si important que certain chercheur ont consacré leur vie entière à la conception de nouvelle feature ou d'attribut caractéristique de texture.
C'est notemment le cas de ce cher Professeur Robert haralick qui a consacré une partie de sa vie à l'analyse des texture en utilisant la matrice de co-occurence qu'il à lui même inventé et publié dans cet article de recherche : Textural features for image classification.
Connu également sous le nom de Gray Level Co-occurence matrix ou GLCM.
Dans cet article, nous verrons :
Qu'est ce que la matrice de co-occurence ( GLCM ) et
comment calculer
Qu'elle sont les différentes mesures statistique qu'il est possible d'extraire de cette matrice et leur signification
Comment calculer la matrice de co-occurence en se servante de la bibliothèque skimage en python
Tu ne le sais peut-être pas encore mais il existe différente approche pour caractériser une texture.
Il y a
Cette approche s'appuie sur la recherche de motif particulier dans une image et sur la quantification de l'apparitions de ces dernier pour caractériser la texture. Elle est particulièrement utiliser pour la caractérisation des
telles que celle présentée ci-dessous.



L'étude de
est une méthode que l'on peu classer dans cette approche.
-L’approche
s’intéresse au fréquences des interactions qu’il existe entre les différents pixels ou les différentes région d’une image. Parmi les méthode utilisant cette approche nous pouvons citer



-L’approche
est divisée en trois catégorie, celle basé sur l’apprentissage de vocabulaire texturale, sur l’extreme learning et celle basée sur le deep learning. Parmi les algorithme utilisé dans cette catégorie nous retrouvons
Pour finir , celle qui nous intéresse dans cette article, il s'agit de
elle utilise les relations statistique qu’il existe entre chaque pixel et leur voisinage pour caractériser une texture.
Parmi les méthodes de cette catégorie, nous retrouvons :
Cette approche est particulièrement utilisé pour caractériser les micro-texture.



Comme je l'ai dit ci-dessus, la matrice de coo-curence est une
Elle est construite en comptant le nombre de fois que 2 pixel de même valeur apparaissent à une même distance et dans une même direction fixé par l’utilisateur .
Pour ce faire la matrice de co-occurence a principalement besoin de 2 paramètre : la direction et la distance.
Par exemple, construire la matrice de co-occurence à 0 ° pour une distance égale à 1 consiste à compter le nombre de fois qu'un pixel et que son premier voisin à droite apparait, puis mettre le total dans la matrice.
For example :
distance=1
img 0°
0 1 3 2 2 1 1 1
1 2 2 3 1 0 3 1
0 0 2 1 1 3 2 3
1 2 3 0 1 1 3 0
Si l'on réitère l'expérience précédent avec une distance de 3, cela revien à qu'un pixel et que son troisième voisin à droite apparait, puis mettre le total dans la matrice.
distance=3
img 0°
0 1 3 2 2 1 1 1
1 2 2 3 1 0 3 1
0 0 2 1 1 3 2 3
1 2 3 0 1 1 3 0
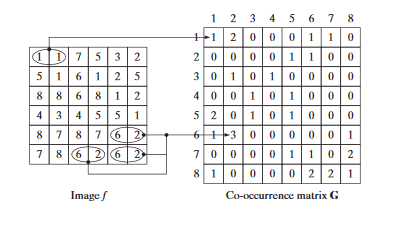
L’image ci-dessous est un exemple de cela 6 puis 2 apparaisse 3 fois dans l’image f, par conséquent dans la matrice de coocurence G les pixel à l’ordonnée 6 et à l’abscisse 2 aura pour valeur 3. A contrario 1 puis 1 apparaît qu’une seul fois.


A l’identique des images, il est possible de calculer les moments de la matrice de co-occurence avec la formule suivante :
Maximum probability
La plus forte co-occurence présente dans l’image.
Dissimilarité
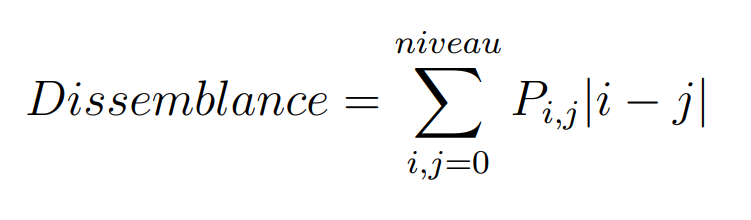
.
Correlation
La corrélation indique le degré de liaison linéaire qu’il existe les différentes occurrences de l’image.
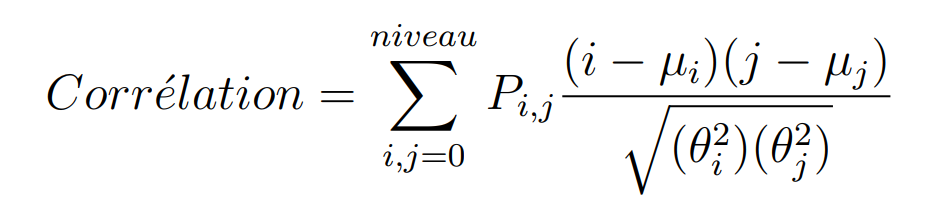
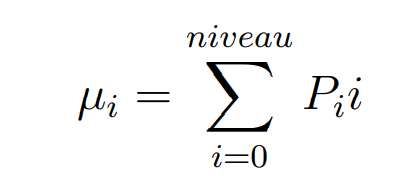
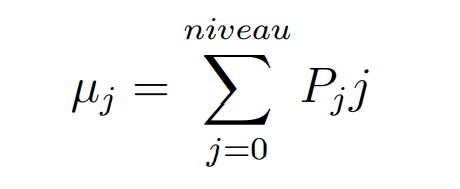
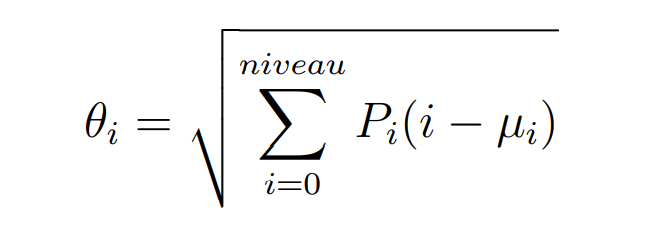
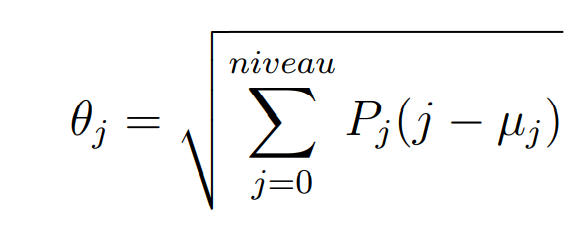
Contrast
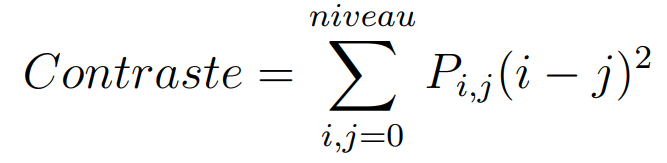
Le contraste permet de mesurer les variations locales des niveaux de gris.
Si tu ne le sais pas, le contraste de la matrice de co-occurence te permet de savoir
si tu est en présence d’une texture plate et monotone. En effet si tout les pixel ont la même valeur ou des valeur proche dans la direction et à la distance que tu a choisi pour construire ta matrice de co-occurence
Il y a fort à parier que la texture soit plate et monotone.
A l’inverse si le matrice est dispersé (étalé autour de la diagonale) et peut remplit en diagonal, le constraste aura une force valeur, et nous serons probablement en présence d’une texture fine.
Uniformity
Cette valeur est d’autant plus élevée qu’une même occurrence de niveau de gris apparaît dans la texture.
Homogeneity
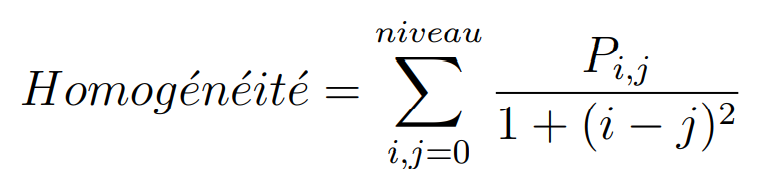
Measures the spatial closeness of the distribution of elements in G to the diagonal.
L’homogénérité, est une mesure qui va te dire si ta texture est homo similaire, avec le même niveau de gris un peu partout sur l’image, plate, ou au contraire si sur l’image, tu est en présence de niveau de gris vraiement différent.
Plus sur l’image, nous seront présence de niveau de gris différents, plus la texture paraîtra cahotique, disparate plus l’homogénéité sera faible.
Inversement, plus l’homogénéité
L’homogénéité donne une idée des similarités locales.
Il reflète l’existence de plages uniformes de texture et affecte un poids de plus en plus faible au fur et à mesure qu’on s’éloigne de la diagonale principale.
Plus la valeur de l’homogénéité est élevée, plus la texture est grossière.
Entropie
Basiquement, l’entropie est une mesure du désordre qu’il existe dans une série de donnée. Plus la texture est dispersé, moins il y a la même occurrence de pixel dans une même image plus cette valeur sera forte. À l’inverse plus la texture sera granulaire, composé d’occurence de couple de pixel différents, plus son désordre sera grand et plus la valeur de l’entropie sera grande.
.
Ils est possible de calculer les matrice de co-occurence en utilisant la fonction greycomatrix de skimage.
greycomatrix(image, distances, angles, levels=None, symmetric=False, normed=False)
Elle prend en paramètre l'image dont on souhaite calculer la matrice de co-occurence, la distance, la direction sous forme d'angle, levels corresponds le nombre de niveau de gris dans l'image d'origine. Symmetric est un paramètre non important, qui indique si l'on souhaite compter à la fois la paire de pixel (i,j) et (j,i). Dans le cas où ce paramètre est True, lors ce que la paire de pixel (i,j) sera rencontré, la position de la matrice correspondant à (i,j) sera incrémenté, mais également, la position correspondant à la paire (j,i).
En générale 256 car elle est souvent codé sur 8-bit, normed indique si l'on souhaite que la matrice de co-occurence retourné par la fonction soit normalisé c'est à dire comprisent entre 0 et 1. Dans le cas où la matrice de co-occurence est normalisée, elle est invariante à la taille de l'image et donc peut servir dans le cas où l'on souhaite comparer deux texture similaire mais de taille différente. A contrario si l'on a deux objets différents de même texture mais de taille différent, il vaut mieux que la matrice ne soit pas normaliser, cela permettra de les différencier.
glcm = greycomatrix(patch, distances=[5], angles=[0], levels=256, symmetric=True, normed=True)
Code complet :
#importation des bibliothèques nécessaire
import cv2
import matplotlib.pyplot as pyplot
from skimage.feature import greycomatrix, greycoprops
import numpy as np
def convert_glcm(glcm):
cpy_glcm=[]
for kol in range (0, 256):
cpy_glcm.append ([])
for kal in range (0,256):
cpy_glcm[kol].append (glcm[kol][kal][0][0])
return np.array(cpy_glcm)
#Ouverture des images
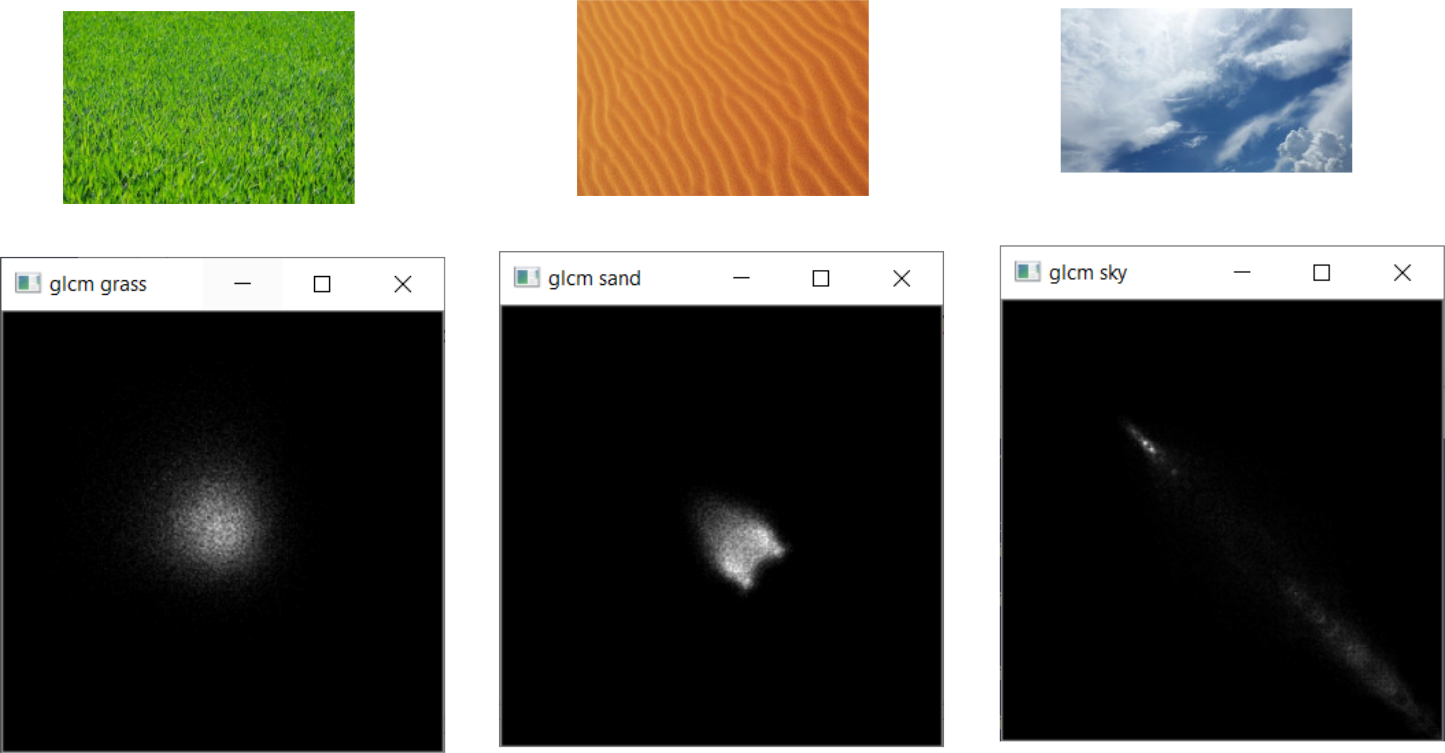
imggrass=cv2.imread ("grass.jpeg",0)
imgsand=cv2.imread ("sand.jpeg",0)
imgsky=cv2.imread ("sky.jpeg",0)
#Calcul des matrices de co-occurence des différentes images
glcmgrass = greycomatrix(imggrass, distances=[5], angles=[0], levels=256,
symmetric=True, normed=True)
glcmsand = greycomatrix(imgsand, distances=[5], angles=[0], levels=256,
symmetric=True, normed=True)
glcmsky = greycomatrix(imgsky, distances=[5], angles=[0], levels=256,
symmetric=True, normed=True)
#Normalisation des matrices de co-occurence des images afin de pouvoir les afficher
img_glcmgrass=cv2.normalize(np.array(glcmgrass), None, 0, 255, cv2.NORM_MINMAX, cv2.CV_8U)
img_glcmsand=cv2.normalize(np.array(glcmsand), None, 0, 255, cv2.NORM_MINMAX, cv2.CV_8U)
img_glcmsky=cv2.normalize(np.array(glcmsky), None, 0, 255, cv2.NORM_MINMAX, cv2.CV_8U)
#Conversion des matrices de co-occurences des images afin de pouvoir les afficher
img_glcmgrass=convert_glcm(img_glcmgrass)
img_glcmsand=convert_glcm(img_glcmsand)
img_glcmsky=convert_glcm(img_glcmsky)
#Affichage des matrices de co-occurences des différentes images
cv2.imshow("glcm grass", img_glcmgrass)
cv2.imshow("glcm sand", img_glcmsand)
cv2.imshow("glcm sky", img_glcmsky)
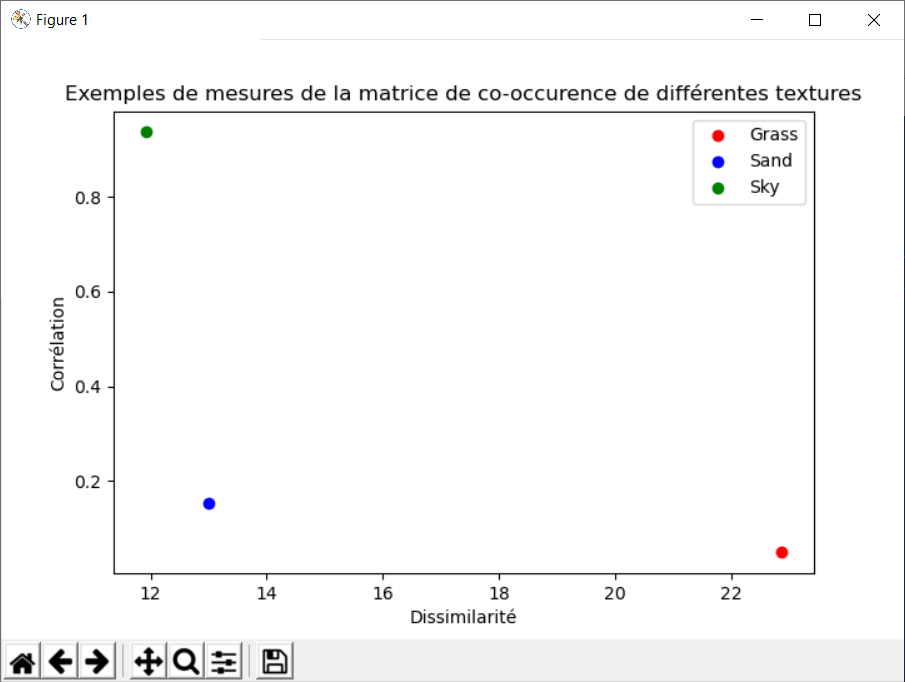
#Calcul à partir de la dissimilarité et de la corrélation de chacune des matrices de co-occurences
dissimilarite_grass=greycoprops(glcmgrass, 'dissimilarity')[0, 0]
correlation_grass=greycoprops(glcmgrass, 'correlation')[0, 0]
#insertion de la dissimilarité et de la corrélation dans un tableau afin de pouvoir les afficher avec la fonction scatter de matplolib
tableau_grass=[[dissimilarite_grass],[correlation_grass]]
dissimilarite_sand=greycoprops(glcmsand, 'dissimilarity')[0, 0]
correlation_sand=greycoprops(glcmsand, 'correlation')[0, 0]
tableau_sand=[[dissimilarite_sand],[correlation_sand]]
dissimilarite_sky=greycoprops(glcmsky, 'dissimilarity')[0, 0]
correlation_sky=greycoprops(glcmsky, 'correlation')[0, 0]
tableau_sky=[[dissimilarite_sky],[correlation_sky]]
#Affichage de la corrélation et de la dissimilarité pour les trois images
pyplot.scatter(tableau_grass[0],tableau_grass[1],label='Grass',color='r')
pyplot.scatter(tableau_sand[0],tableau_sand[1],label='Sand',color='b')
pyplot.scatter(tableau_sky[0],tableau_sky[1],label='Sky',color='g')
pyplot.xlabel('Dissimilarité')
pyplot.ylabel('Corrélation')
pyplot.title('Exemples de mesures de la matrice de co-occurence de différentes textures')
pyplot.legend()
pyplot.show()