La segmentation permet de mettre en évidence et d’isoler les différents objets présents dans une image.Il existe différentes méthodes de segmentation (le seuillage, la classification, le clustering, les level-set, graph-cut, etc .…).Dans cet article j’aborderais avec vous le seuillage et plus particulièrement le seuillage automatique avec la méthode d’Otsu.
Bien que je vais vous expliquer le fonctionnement de la méthode d’Otsu, pour l’utiliser il vous sera nécessaire d’utiliser OpenCV python. Si vous ne connaissez pas, OpenCV, je vous recommande de jeter un coup d’œil au tutoriel d’initiation à OpenCV que j’ai écrit.
Le seuillage est une opération qui permet de transformer une image en niveau de gris en image binaire (noir et blanc), l'image obtenue est alors appelée masque binaire. Il existe 2 méthodes pour seuiller une image, le seuillage manuel et le seuillage automatique.
En pratique, le seuil optimal est considéré comme étant celui qui sépare le mieux le fond et les objets présents sur l’image. L'image ci-dessous illustre ce principe.
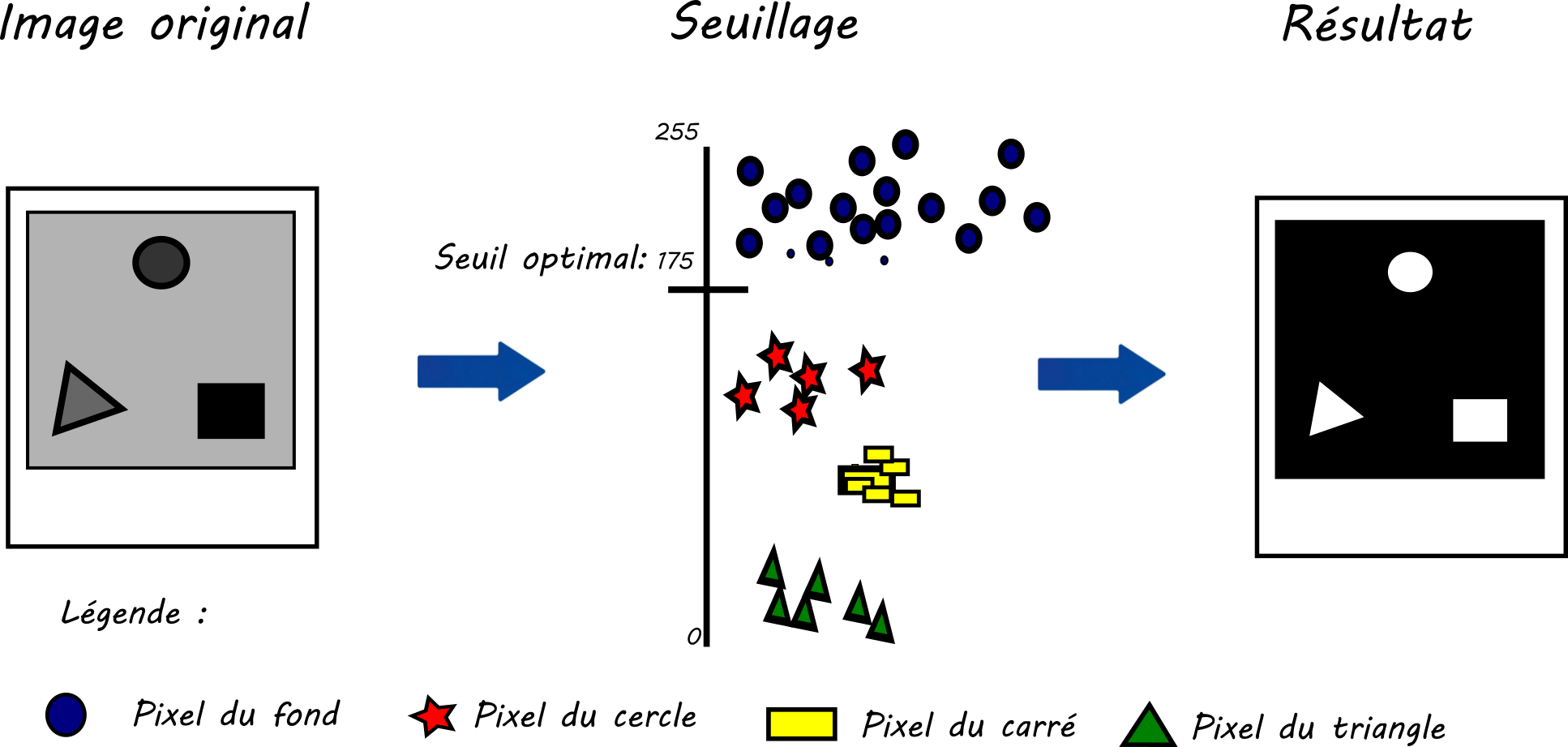
Seuillage optimal
Dans cet exemple, le seuil idéal est 175, car il permet de mettre en évidence tous les objets présents dans l’image.
Pour utiliser le seuil manuel avec OpenCV, il suffit d’appeler la fonction thresold comme suit :
ret,th=cv.threshold(img, seuil,couleur, option)
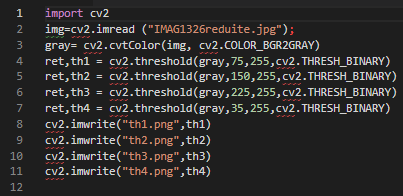
Elle prend en paramètre, img : l’image à traiter , seuil : la valeur du seuil , couleur : la couleur que l’on souhaite attribuer à la zone objet et elle retourne ret : la valeur du seuil, et th : l’image binaire résultat du seuillage. Afin d’illustrer cela, dans le code suivant, j’ai seuillé l’image fleur.png préalablement passée en niveau de gris avec quatre seuils : 35,75,150,225.

fleur.png
 Résultat du seuillage
Résultat du seuillage
Nous remarquons que le seuillage n’a pas fonctionné, quel que soit le seuil. En effet, les pixels du fond sont mélangés au pixel des fleurs. C’est pour cela qu’il est préférable de passer l'image dans l’espace HSV avant de seuiller.
Soit 2 classes de pixels C1 et C2. La classe 1 (C1) est définie comme étant composée des pixels ayant une valeur comprise entre 0 et k avec k<255. Le reste (classe C2) des pixels compris entre k et 255 (inclus) faits partit de la seconde classe. Le but du jeu est de trouver "k" tel qu’il sépare au mieux le fond et les objets de l'image traitée.
Afin de trouver "k", la méthode d’Otsu va calculer la variance interclasses entre C1 et C2 pour tous les k possibles (de 0 à 255). La variance interclasses caractérise la dissemblance qu’il existe entre les pixels des deux classes. Plus elle est haute, moins les deux classes se ressemblent. La réciproque est également vraie.
Par conséquent, le seuil optimal est le k obtient la plus haute variance interclasse.
Maintenant que je vous ai montré comment elle fonctionne en principe, nous allons voir comment l’implémenter. Les étapes de l’algorithme d’Otsu sont les suivantes :
1- Construction de l’histogramme des niveaux de gris de l’image.
2-Normalisation de l’histogramme obtenu en 1. Normaliser l’histogramme, permet d’obtenir un histogramme dont toutes les valeurs sont comprises entre 0 et 1. Le calcul ci-dessous permet d’y parvenir :
f(x)=(x-min)/(max -min)
Formule normalisation
avec x étant la valeur en ordonnée de l’histogramme que l’on souhaite transformer, min et max étant respectivement la valeur minimale et maximale en ordonnée de l’histogramme Le pseudo-code permettant d’obtenir la normalisation est présenté ci-dessous :
N = taille_image (image) ;
hist=histogramme(image)
for col in hist :
col=col/N
Remarque : en normalisant l’histogramme des couleurs, l’on obtient une distribution de probabilité. Par exemple la probabilité que dans notre image il y ait un pixel dont le niveau de gris est 255 est la valeur de notre histogramme normalisé pour l’abscisse 255.
3-Calcul de la probabilité qu’un pixel de l’image appartienne à C1. Cela est fait en calculant la somme de toutes les colonnes de l’histogramme comprises entre 0 et k.
4-Calcul de la probabilité qu’un pixel de l’image appartienne à C2. En faisant simplement 1- proba(C1) calculé dans l’étape précédente.
5- Calcule de la variance interclasses entre C1 et C2 grâce à la formule :
avec Moy étant la moyenne de l’image, ProbaC1(k) étant la probabilité qu’un pixel de l’image appartienne à C1, Moy(k) la moyenne des pixels de la classe C1.
6- Les étapes 2,3,4,5 sont répétées pour toutes les valeurs de k possible.
La fonction python permettant d’utiliser cet algorithme est la fonction thresold. Je ne vais pas la présenter, car je l’ai présenté précédemment et seuls le second (il passe à 0) et le dernier paramètre changent (+ cv.THRESH_OTSU a été rajouté) .
ret2,th2 = cv.threshold(img,0,255,cv.THRESH_BINARY+cv.THRESH_OTSU)
Exemple : Application de la méthode d’Otsu sur chaque canal de l’image HSV

Image de départ
import cv2 as cv
import numpy as np
img=cv.imread ("IMAG1326.jpg");
hsv = cv.cvtColor(img, cv.COLOR_BGR2HSV)
h,s,v= cv.split(hsv)
ret_h, th_h = cv.threshold(h,0,255,cv.THRESH_BINARY+cv.THRESH_OTSU)
ret_s, th_s = cv.threshold(s,0,255,cv.THRESH_BINARY+cv.THRESH_OTSU)
ret_v, th_v = cv.threshold(s,0,255,cv.THRESH_BINARY+cv.THRESH_OTSU)
cv.imwrite("th_h.png",th_h)
cv.imwrite("th_s.png",th_s)
cv.imwrite("th_v.png",th_v)
Résultat :

Seuillage d'Otsu sur le canal hue


Les seuils optimaux trouvés par Otsu pour les canaux teinte, saturation et luminosité sont respectivement 75, 168 et 114.
Remarquons que, la segmentation obtenue sur le canal luminosité n’a rien donné d’intéressant.
Celle du canal hue a permis d’extraire les fleurs blanches.
Enfin celle de la saturation a extrait toutes les fleurs sauf les blanches.
Afin d’obtenir une segmentation parfaite qui sépare toutes les fleurs du fond, il nous est nécessaire de fusionner le résultat obtenu en hue et en saturation.
Cette opération se fera par l’intermédiaire d’opérateurs binaires d’image.
float compute_first_order_cumulative_moment(float *hist, int k)
{
float first_order_cumulative_moment = 0;
for (int i = 0; i < k; i++)
{
first_order_cumulative_moment += i*hist[i];
}
return first_order_cumulative_moment;
}
float compute_variance_class_separability(float uT,float wk, float uk)
{
return pow((uT*wk-uk),2)/(wk*(1-wk));
}
void otsu(Mat img)
{
int s;
float hist[256];
for (int i = 0; i < 256; i++)
{
hist[i] = 0;
}
for (int i = 0; i < img.rows; i++)
{
for (int j = 0; j < img.cols; j++)
{
hist[img.at<uchar>(i, j)] += 1;
}
}
int N = img.cols*img.rows;
for (int i = 0; i < 256; i++)
{
hist[i] = hist[i] / N;
}
float w[256],u[256],uT;
for (int i = 0; i < 256; i++)
{
w[i] = compute_zero_order_cumulative_moment(hist, i);
u[i] = compute_first_order_cumulative_moment(hist, i);
}
uT = compute_first_order_cumulative_moment(hist, 256);
float variance_class_separability_max = -1;
float best_threesold = 0;
for (int i = 0; i < 256; i++)
{
int vk = compute_variance_class_separability(uT, w[i], u[i]);
if (vk > variance_class_separability_max)
{
variance_class_separability_max = vk;
best_threesold = i;
}
}
for (int i = 0; i < img.rows; i++)
{
for (int j = 0; j < img.cols; j++)
{
if (img.at<uchar>(i, j) < best_threesold)
{
img.at<uchar>(i, j) = 0;
}
else
{
img.at<uchar>(i, j) = 255;
}
}
}
}
https://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=4310076
https://en.wikipedia.org/wiki/Otsu%27s_method