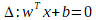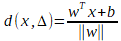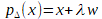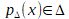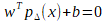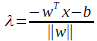Si il y a un modèle de machine learning qui m'a donné du fil à retordre, c'est bien les support vector machine ou encore machine à vecteur support en français.
Je me rappelle encore quand j'étais chez ma mamie, à essayer de les implémenter from scratch pour faire de la reconnaissance vocale.
Ou encore, je me rappelle du regard de mes étudiants un peu perdu quand je leur faisais le cours de programmation quadratique !
Il en ont bien bavé avec moi, surtout quand je leur ais dit que le projet de fin de semestre consistait à construire une svm.
Cela me fait rire en écrivant c'est ligne !
Mais le plus ironique de tout cela est que les support vector machine sont un modèle de machine learning relativement simple, c'est l'entraînement qui complique les choses.
La machine à vecteur support est un algorithme qui maximise la frontière de séparation entre les échantillons les plus proches de classes différentes. Comme montré sur la figure IV.5, pour un problème à N dimension la suport vertor machine va chercher l’hyperplan qui sépare le mieux nos classes. Il s’agit de l’hyperplan pour lequel la marge de séparation est maximale.
Afin de pouvoir traiter des cas où les données ne sont pas linéairement séparables, la SVM transforme l'espace de représentation des données d'entrées en un espace de plus grande dimension (possiblement de dimension infinie), dans lequel il est probable qu'il existe une séparatrice linéaire.
Les SVM font partis avec les machine de Boltzmann par exemple des modèle qui reposent sur un support théorique et fondamentale fort.
Je dis cela car, théoriquement Vapnik, l'inventeur des SVM à prouvé que les support vector machine était capable de trouver la séparation optimale entre les exemple d'une classe A et ceux d'une classe B.
Pour ce faire, l'idée derrière les SVM consiste à construire un hyper plan qui séparera les deux classe dans le plan.
Bonne idée, avec les framework mathématique existant sur les hyperplan à l'époque de vapnik, il fut inspiré.
Et pour faire cours, il s'est dit qu'il allait représenter une situation de classification sous forme de problème quadratique.
L'idée, trouver l'hyperplan optimal qui séparera à fond les deux classe !
Seul hic de cette idée. Elle ne peut ête utilisé que pour séparer deux classe.
Mais à propos, c'est quoi un problème de programmation quadratique ?
Un prblème de programmation quadratique est un problème que l'on peut exprimer sous la forme :
En quoi séparer des hyperplan est un problème de programmation quadratique ?
Comment est t'il possible de résoudre le fait que la SVM ne peut séparer que deux classe ?
Une des méthodes les plus couramment utilisée et les plus efficace est la classification OVO.
Ainsi pour résoudre un problème de classification à n classes on va calculer k (k-1) classifieurs,
chacun de ces classifieurs étant un classifieur simple, entre les différentes classes 2 à 2 en
ignorant les autres classes à chaque fois (la classe 1 avec la classe 2 puis la 1 avec la 3 et enfin la
2 avec la 3 pour un problème à 3 classes)