Et Hop, nous voilà repartis ensemble dans un nouvel article, cette fois-ci sur les arbres de décision !
Quand l'on débute en machine learning, les arbres de décision, également connue sous le nom de Classification and regression trees (CART) dans le monde anglophone, sont certainement l'un des meilleurs modèles par lesquels comment et pour cause c'est le seul modèle comme on le verra par la suite dans cet article qui permet la compréhension de la modélisation construite.
En effet, puisque pour comprendre, l'arbre de décision il suffit de le représenter graphiquement ou même textuellement comme je vais le montrer dans la suite afin d'observé les choix opérés par l'algorithme d'entraînement et ainsi avoir une compréhension bien plus profonde du problème que celles que l'on aurait pu avoir si l'on avait choisi d'utiliser un autre modèle tels qu'un classique perceptron multicouche ou pire encore une support vector machine (Je ne vous dis pas le mal de crâne pour déchiffrer les maths derrière ces 2 boites noires).
En plus de permettre une bonne compréhension du modèle, un des grands avantages des arbres de décision est leur capacité à gérer des données non numériques telles que les chaînes de caractères sans encodage préalable. Contrairement un réseau de neurones ou il faut un encodage de type latent dirichlet allocation ou encore Word2Vec afin de pouvoir utiliser le modèle.
Quoi qu'il en soit dans cet article, nous verrons :
Qu'est-ce qu'un arbre de décision
Comment est entraîné un arbre de décision
Comment créer un arbre de décision et l'afficher à l'aide de sklearn

Son nom est assez explicite et à vrai dire si vous avez fait des études d'informatique et bien compris la notion d'arbres de graphe vous verrez que ce concept est assez simple.
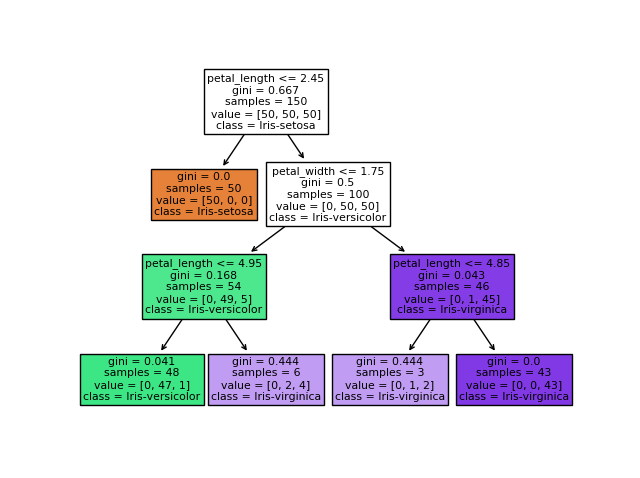
L'idée c'est de modéliser la solution du problème de machine learning que l'on traite comme une suite de décision à prendre. Une décision étant représentée par une feuille dans l'arbre. Comme montré ci-dessous ou l'on décide que la fleur est une Iris viginica si elle a une longueur de pétale supérieur " petal width" > 1.75 sinon c'est une Iris-versicolor.

Autre exemple. Supposons qu’aujourd’hui, vous vouliez aller pique-niquer avec votre compagne et vos enfants. Tout d'abord vous allé vérifier qu'il fait beau, par la suite vous allé demander à votre compagne si ça lui-di de pique-niquer si oui, vous allez demander à vos enfants si eux aussi ils sont OK pour pique-niquer et si c'est le cas, vous piquerez avec votre compagne ou compagnon. L'arbre de décision correspondant aux concepts que j'ai énoncé précédemment est le suivant :
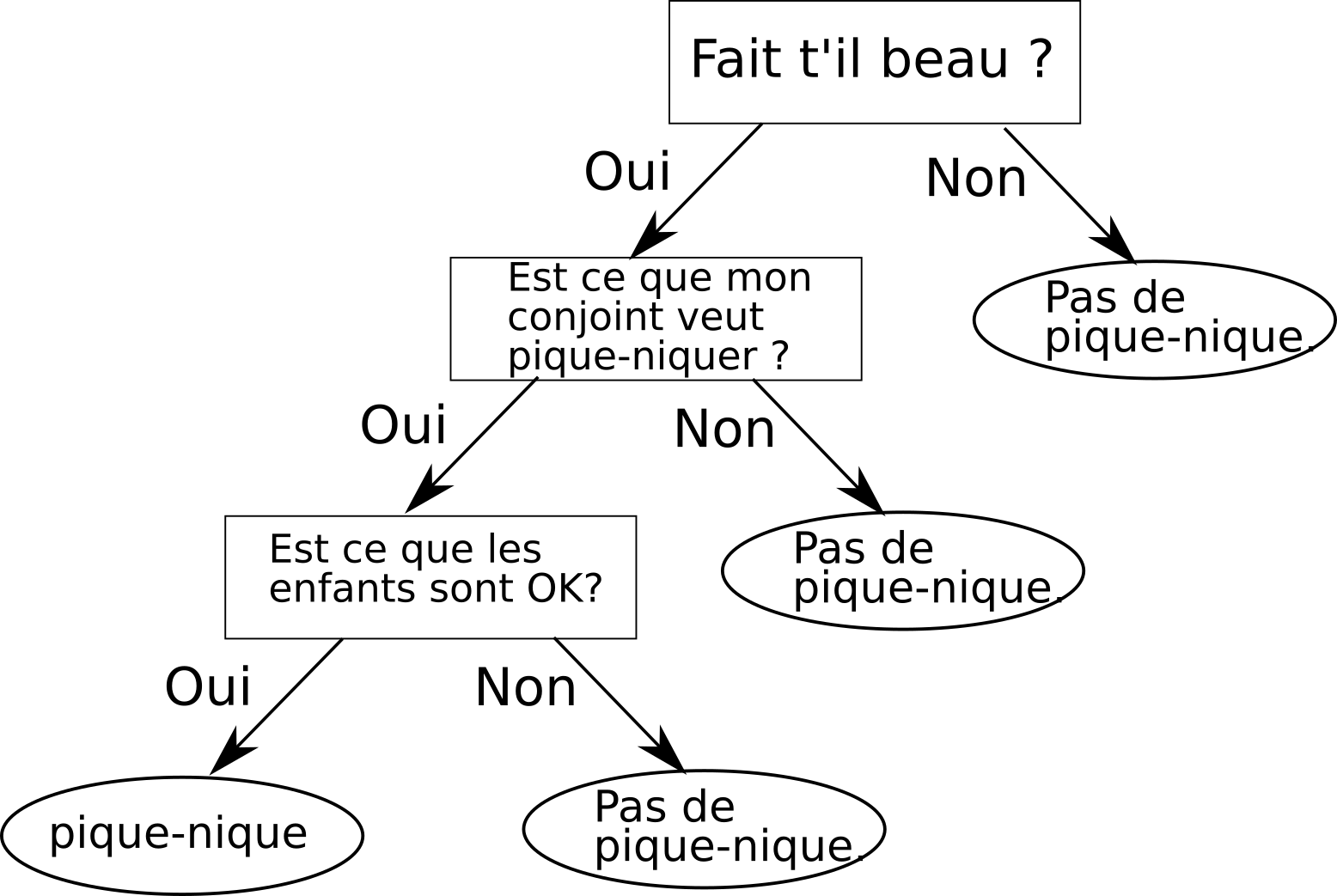
Un arbre de décision est entraîné à la gloutonne si tu me le permets !
Deux cas sont possibles le cas de la classification et le cas de la régression, mais dans les deux cas la manière d'entraîner reste la même, seule change la mesure qui permet de mesurer la qualité des nouvelles branches créées.
Mais dans un premier temps, je vais voir avec toi le cas de la classification, car je t'avoue que c'est probablement plus simple pour la suite de voir ce cas-là.
Pour la classification, à chacune de ces itérations, l'algorithme d'entraînement va rajouter la décision qu'il lui semble le mieux de rajouter. Pour ce faire, il va tester et évaluer la qualité de toutes les nouvelles décisions qu'il est possible d'ajouter à l'arbre en calculant le score Gini. Le score Gini est un score qui a été spécialement inventé afin de réaliser la sélection des nouvelles branches dans un arbre de décision.
Le score "Gini", est compris entre zéro et 1. Il s'agit d'une valeur numérique indiquant la probabilité que l' arbre se trompe lors de la prise d'une décision ( par exemple qu'il choisit la classe "A" alors que la vraie classe c'est "B").
Il est utilisé quasi systématiquement (dans les bibliothèques populaires de machines learning tel que sklearn) utilisé pour estimer la qualité d'une branche.
Une branche sera rajoutée à l'arbre si parmi toutes les branches qu'il est possible de créer cette dernière présente le score Gini maximal.
Il est possible d'obtenir le score Gini, grâce à la formule suivante :
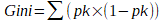
ou pk est la probabilité d’obtenir la classe k.
Si l'on reprend l'exemple du pique-nique présenté ci-dessus, le score "Gini" vaudra :
P_pique_nique x (1 - P_pique_nique) + P_non_pique_nique x (1 - Pnon_pique_nique)
1- À l'initialisation, l'arbre est totalement vide.
2- Le score de toutes les décisions qu'il est possible de prendre est calculé.
3- La décision qui présente le score Gini maximal est choisie comme racine
4-Tant qu'il est possible de faire un split et que le critère d'arrêt n'est pas respecté
5- Pour chaque décision qu'il est possible d'ajouter à l'arbre; Faire 6.
6- Calcul du score Gini de la décision courante
7-Sélection de la décision admettant le score max et ajout de celle-ci à l'arbre
Il existe de nombreuses conditions d'arrêt possible pour cet algorithme d'entraînement, mais les plus populaires sont les suivantes :
La "maximum tree depth" qui signifie profondeur maximale de l'arbre, il s'agit d'arrêter le développement de l'arbre une fois qu'il a atteint une certaine profondeur, cela évitera que l'arbre construise des branches avec trop peu d'exemples et donc permettra d'éviter un sur apprentissage.
Le "minimum sample split" ou encore nombre d'exemples minimum pour un split consiste à ne pas splitter une branche si la décision concerne trop peu d'exemples. Cela permet également d'empêcher le surapprentissage.
Pour finir, il est également possible de ne pas choisir de critère d'arrêt et de laisser l'arbre se développer jusqu'au bout. Dans ce cas il s'arrêtera que quand il n'y aura plus de split possible. Généralement, quand il n'y a pas de critère d'arrêt, il n'est pas rare qu'un élagage de l'arbre ,ou "pruning" en anglais s'en suive. Élagage consistant à éliminer tous les splits n'améliorant pas le score
Pour la régression c'est généralement l'erreur quadratique moyenne ou mean squarred error qui est employée.
Son calcul est simple, c'est la moyenne de toutes les erreurs commises par l'arbre il s'agit de la moyenne de la valeur absolue de la différence constatée entre la prédiction et la vraie valeur.
MSE= somme ( ( y_prédit - y_vrai) ^2)/nombre_de_prédictions
C'est à dire au début l'arbre
Pour créer un arbre de décision en python, il te faudra faire appel à la bibliothèque scikit-learn.
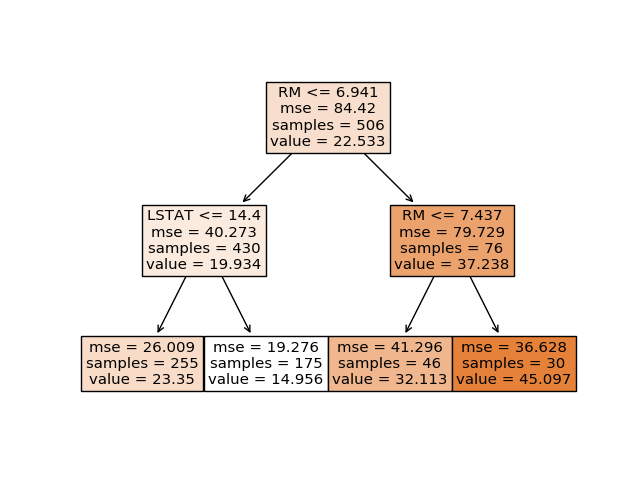
Le concept des forêts d'arbres décisionnels consiste à utiliser un ensemble d'arbres décisionnels afin de prendre une meilleure décision que si un seul arbre décisionnel avait été choisi. Lire l'article sur le Random Forest "Forêt d'arbres décisionnels".
[Moro et al., 2014] S. Moro, P. Cortez and P. Rita. A Data-Driven Approach to Predict the Success of Bank Telemarketing. Decision Support Systems, Elsevier, 62:22-31, June 2014