Il y a de multiples raisons d'utiliser Scikit-Learn qui sont simples et évidentes.
-Scikit-Learn est simple d'utilisation et puissante
En effet, le nom des fonctions est simple et relate effectivement leur rôle (ex : fit pour entrainer un modèle (traduction littérale du verbe entraîner en français), eval pour évaluer un modèle. Simple ! Non ? ;-))
-Scikit-Learn est gratuite ce qui probablement doit plaire à beaucoup de sa communauté
-Le fait d'être gratuite ne l'empêche aucunement d'être puissante, quoi de plus normal pour une bibliothèque énormément utilisée par de gros industriels et de nombreuses universités tels que Evernote, Inria, spotify, etc....
-Ses sources sont modifiables et accessibles à l'adresse suivante https://github.com/scikit-learn/scikit-learn.
-Je rajouterai à cela, que tous les algorithmes et modèles présents dans cette librairie le sont en version optimisés.
C'est actuellement la bibliothèque de machine learning la plus complète et la plus vaste à ma connaissance. Et je pense bien personnellement qu'actuellement elle est la meilleure librairie python de machine learning.
En machine learning, il existe grosso modo 6 catégories de problème qui sont : la classification, la régression, le clustering, la réduction de dimensionnalité, le tuning de modèle et le prétraitement de données.
La classification est l'art d'attribuer automatiquement une classe à des données dont on ne connait pas la classe en se servant de données similaires déjà classées.
La régression permet de mettre en place des modèles capables de prédire des valeurs numériques telles que le prix du pétrole, d'action en bourse ou tout simplement la consommation d'électricité à partir des données fournies en entrée du modèle. Il s'agit d'un algorithme d'apprentissage supervisé, c'est-à-dire que préalablement à la prédiction il faudra d'ores et déjà l'entraîner avec des données similaires.
Le clustering est l'art de regrouper automatiquement des données sans entraînement préalable. C'est donc une tâche de classification non supervisée.
La réduction de dimensionnalité permet de transformer des vecteurs de caractéristique de grande dimension (ex : > 1000) en vecteur de caractéristique de petite dimension (ex :<10). Elle met en valeur les informations essentielles contenues dans les données.
Le tuning de modèle consiste à trouver le meilleur modèle possible avec les meilleurs hyperparamètres possibles pour résoudre un problème de machine learning.
Le prétraitement des données permet d'effectuer les opérations nécessaires avant extraction d'information ou envoi des données dans un classifieur (ex : suppression de bruit).
Scikit-learn n'est disponible qu'en python. Ce qui est un peu dommage, d'autant plus que le langage python est loin d'être un des plus économes.
J'avais lu un jour sur un article de developpez.com que celui-ci était 76 fois si je ne me trompe pas plus énergivore que le langage C.
Je ne vous cache pas les émissions de CO2 que ça doit faire !
Python le langage le plus polluant de la terre XD.
Je délire un peu :-) ! Ceci dit l'info est vraie.
Retournons aux choses sérieuses. Pour ceux qui n'auraient pas déjà installé Python, il est possible de le télécharger en cliquant sur le lien ci-dessous :
Une fois installé, le gestionnaire de paquet de ce dernier "pip" est directement installé avec.
Du coup, on va pip installer Scikit-Learn.
La commande qui permet d'installer Scikit-Learn est la suivante :
pip install scikit-learn
Cependant, cette ligne de commande n'a jamais marché pour moi avec mon PC, pour la simple et bonne raison que je suis sur Windows et que jusqu’à maintenant je n’ai jamais eu encore le courage de chercher le chemin de l'exe pip pour le mettre dans mon path.
Du coup, à chaque fois que je veux pip installer une bibliothèque je suis obligé de taper ça :
python -m pip install scikit-learn
Je dis ça pour les gens qui sont sur Windows et qui auraient le même souci que moi.
Si tu ne veux pas passer par python et par son gestionnaire de paquet, tu as la possibilité d'installer Anaconda que je te recommande vivement.
Anaconda à la particularité de permettre la création d'environnement de travail dédié à des projets spécifiques.
Je m'explique.
Supposons que tu travailles sur un projet dont tu as repris le code source en ligne, mais qui ne fonctionne qu'avec Scikit-Learn v1 et que la dernière version de Scikit-Learn, c'est la v2 que tu as installée sur ton pc à l'aide de pip.
Plutôt que de désinstaller ta version de Scikit-Learn pour travailler sur ton projet.
Tu peux installer Anaconda, ce dernier te permettra de créer un environnement spécialement dédié à ton projet.
Une fois Scikit-Learn installée, tu peux créer ton premier modèle.
Dans cette partie, nous allons mettre en place un modèle de classification supervisée.
C'est-à-dire que nous allons créer un modèle qui va classer des données après s'être entraîné sur des données déjà classées.
Il y a 4 grandes étapes dans la construction d'un modèle, il s'agit de :
Le chargement et le prétraitement des données d'apprentissage
La mise en place du modèle et la configuration de ces hyperparamètres.
L'entraînement du modèle
L'évaluation du modèle
Il existe différents formats de stockage de données tels que le Json, le TXT ou encore le cSv que nous utiliserons dans ce tutoriel.
Le CSV est un format très connu et largement utilisé chez les data scientist. Il se compose d'une première ligne qui indique les données qui se trouvent dans le fichier et le reste des lignes contient les données.
Quoi de plus simple.
Prenons par exemple, le fichier Iris.csv que nous allons utiliser dans ce tutoriel et que vous pouvez télécharger en cliquant sur le lien Iris.csv. Rapidement, pour expliquer en quoi consiste le jeu de données Iris.csv :
Il s'agit d'un jeu de données constitué à partir de mesures prélevées de fleurs appartenant à 3 espèces différentes (Iris Setosa, Iris versicolore et Iris Virginia).
Il est constitué au total de 150 exemples avec 50 exemples pour chaque espèce.
Les quatre mesures qui ont été prélevées sont : la longueur de sépale, la largeur de sépale, la longueur de pétale et la largeur de pétale.
Voici un extrait du début du fichier :
sepal_length,sepal_width,petal_length,petal_width,variety
5.1,3.5,1.4,0.2,Iris-setosa
4.9,3,1.4,0.2,Iris-setosa
4.7,3.2,1.3,0.2,Iris-setosa
4.6,3.1,1.5,0.2,Iris-setosa
5,3.6,1.4,0.2,Iris-setosa
5.4,3.9,1.7,0.4,Iris-setosa
4.6,3.4,1.4,0.3,Iris-setosa
5,3.4,1.5,0.2,Iris-setosa
Dans l'extrait ci-dessus on peut voir que la première ligne indique qu'il a dans le jeu de données la longueur de sépale, la largeur de sépale, la longueur de pétale, la largeur de pétale et la variété de la fleur.
Pour charger en mémoire le jeu de données, il nous faudra utiliser la librairie python csv.
Il s'agit d'une librairie qui permet de lire, de modifier et d'écrire des fichiers csv simplement.
Elle est par défaut installée avec python.
Dans un fichier csv, la dernière colonne indique généralement la classe et toutes les colonnes avant indiquent les attributs.
Voici le code qui permet de charger en mémoire les données du jeu Iris.
from __future__ import absolute_import, division, print_function, unicode_literals
#Chargement du fichier iris.csv
import csv
iris_data=[]
iris_classe=[]
with open('iris.csv') as csv_file:
csv_reader = csv.reader(csv_file, delimiter=',')
for row in csv_reader:
iris_data.append([float(row[0]),float(row[1]),float(row[2]),float(row[3])])
iris_classe.append(row[4])
Tout d'abord, il faut savoir qu'en machine learning il existe énormément de modèles, et qu'il n'est pas possible de savoir à l'avance qu'elle est le modèle qui obtiendra les meilleurs résultats à l'avance.
Mais d'expérience, je peux dire qu'il existe 3 grandes approches de modèle de classification,
La première consiste à mettre en place un réseau de neurones. C'est la solution la plus populaire de nos jours, non pas parce qu'elle est la plus puissante du moins en ce qui concerne l'utilisation du perceptron multicouche, pour ce qui est des autres réseaux de neurones, nous en reparlerons une autre fois. Mais parce que c'est celle dont on entend le plus parlé dans les médias conséquence tout le monde veut implémenter un perceptron multicouche qui est à ce jour le réseau de neurones le plus simple, mais très peu savent que pour la classification ce n'est pas forcément le plus efficace.
L'approche neuronale est une approche assez particulière, car elle repose uniquement sur la capacité de l'ordinateur à calculer. Jusqu’à présent, c'est le type de modèle qui fonctionne le mieux, mais dont le fonctionnement théorique reste toujours mystérieux aux yeux des chercheurs. Un peu comme pourquoi un avion vole, beaucoup de réponses théoriques on était formulé, mais toute on trouvé des contre thèse et des contre-exemples qui font que jusqu'a maintenant on ne sait pas pourquoi un avion vole même si on sait comment faire un avion voler.
La seconde grande approche qu'il est possible de faire c'est à l'aide des arbres de décision. Il s'agit d'une catégorie d'algorithme qui va prendre une suite de décision les unes après les autres selon les décisions qui ont été précédemment prises j'ai d’ailleurs écrit un article sur le sujet.
Enfin la troisième grande approche est à l'antipode de l'approche neuronale. Il s'agit d'utiliser des modèles mathématiques construits à l'aide des théories existantes et pour lesquels la théorie explique pourquoi, ils fonctionnent. C'est notamment le cas des machines à vecteurs support, mais également des classifieurs de Bayes ou encore de la régression logistique.
Dans ce tuto j'ai décidé d'expérimenter deux approches, la première un réseau de neurones de type perceptron multicouches et la seconde un arbre de décision.
Le perceptron est la brique élémentaire de départ qui a permis l’invention des premiers réseaux de neurones. À l’origine, celui-ci avait été conçu dans les laboratoires du Cornell Aeronautical par Frank ROSENBLATT en 1957 afin de modéliser le fonctionnement d’un neurone humain. Sur le schéma ci-dessous, nous pouvons observer le perceptron. Il possède n entrées (X1 à Xn), ces entrées sont généralement des nombres entiers où réels transmis au perceptron. À chacune des entrées X est associée un poids W qui servira au calcul de la sortie Y. Enfin, une connexion bias est ajoutée, car celle-ci est nécessaire au bon fonctionnement du perceptron. Le calcul effectué pour obtenir la sortie Y est le suivant :
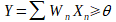
Quand il s’agira de classification binaire, l’on dira que si Y est supérieur à θ, la classe vaut 1 sinon elle vaut zéro.
Schéma du perceptron :
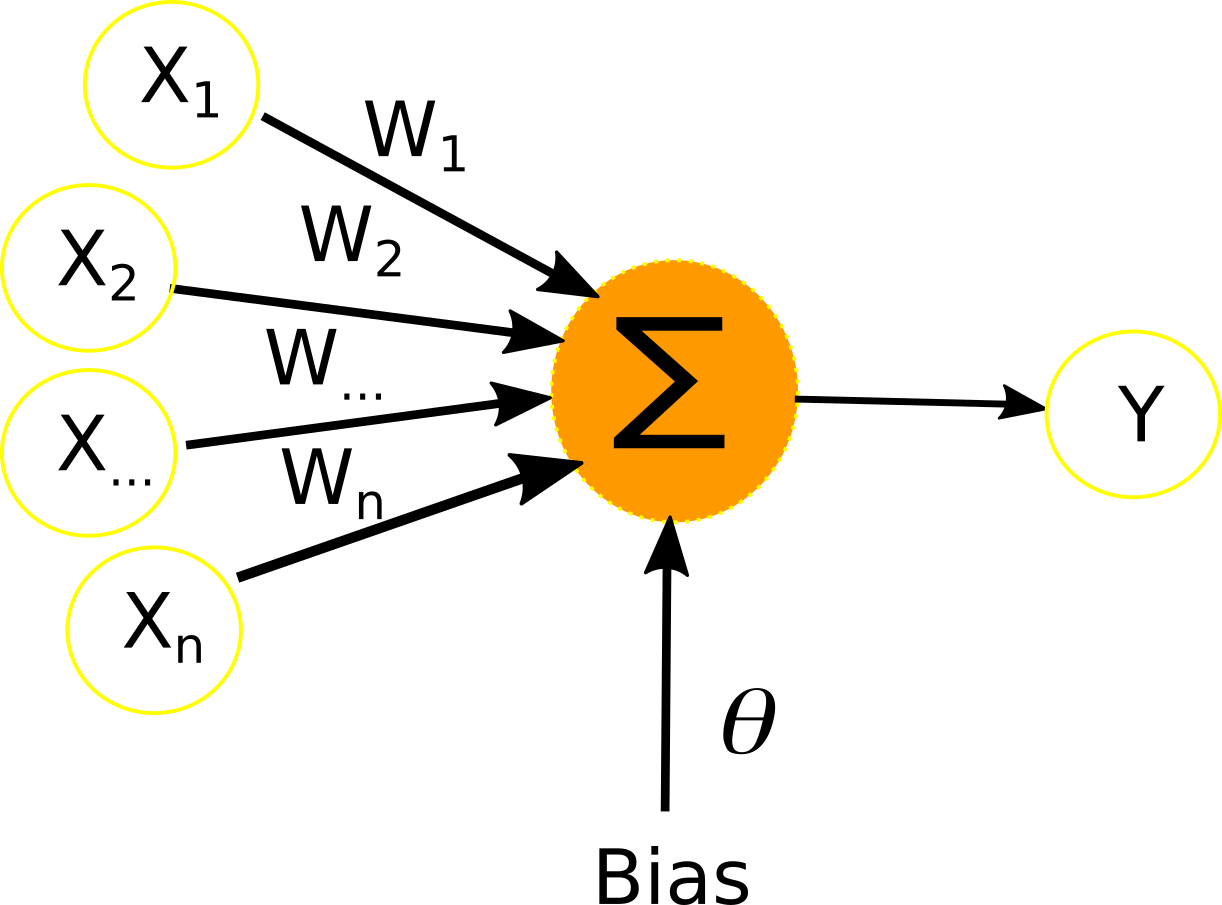
Entraîner un perceptron est relativement simple. Supposons que nous ayons une base B de k exemple, chaque exemple est composé de n mesure X1 à Xn qui sont de nombres réels et d’une sortie c qui est le résultat que l’on souhaite que le perceptron obtienne. L’algorithme qui permet d’entrainer le perceptron est le suivant :
Entrée : Une base constituée B de k exemple
1- Initialisation aléatoire de tous les poids du réseau
2- Choix aléatoire d’un exemple i de la base B
3-Calcul de la sortie Y pour cet exemple avec la formule
4- Actualisation des poids en utilisant la formule : W_j = W_j + (c – Y ) * x_j
L’on peut voir les neurones du perceptron multicouche comme une multitude de perceptron connectés entre eux.La particularité topologique de ce réseau est que tous les neurones d’une couche sont connectés à tous les neurones de la couche suivante. Chaque neurones a donc n entrées, n étant le nombre de neurones présent dans la couche précédente, et une sortie qui est envoyée à tous les neurones de la couche suivante.
À chaque connexion neuronale est associé un poids W, comme pour les entrées du perceptron. Le calcul de la sortie d’un neurone se fait selon la fonction d’activation qui a été choisie.
Schéma du perceptron multi-couche :
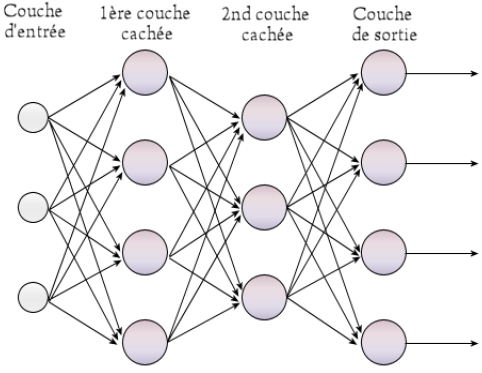
Voici la ligne qui permet de déclarer le perceptron multi-couche.
La classe MLPClassifieur de Scikit-Learn permet de déclarer un classifieur de type perceptron multi-couche. Son constructeur prend en paramètre le solver il s'agit de l'algorithme choisi pour l'entraînement du réseau.
hiddent_layer_sizes il s'agit du nombre de couches cachées et le nombre de neurones par couche cachée.
Random_state il s'agit de l'état aléatoire d'initialisation du réseau. Du fait que les poids sont initialisés aléatoirement le résultat du réseau est amené à varier si l'initialisation de ses poids change. Le paramètre random state permet de faire cela.
Alpha est le pas, la vitesse à laquelle le réseau va apprendre. Plus il sera petit, plus le réseau va prendre du temps pour converger vers la solution du problème, plus il est grand plus le réseau va converger rapidement, mais plus il risque de ne jamais trouver la solution optimale du problème.
L'arbre de décision est l'unité de base qui compose le RandomForest.
Il s'agit d'un modèle simple qui tend à résoudre un problème de machine learning en le modélisant comme une suite de décisions en fonction des décisions qui ont été prises ultérieurement.
Prenons un exemple !
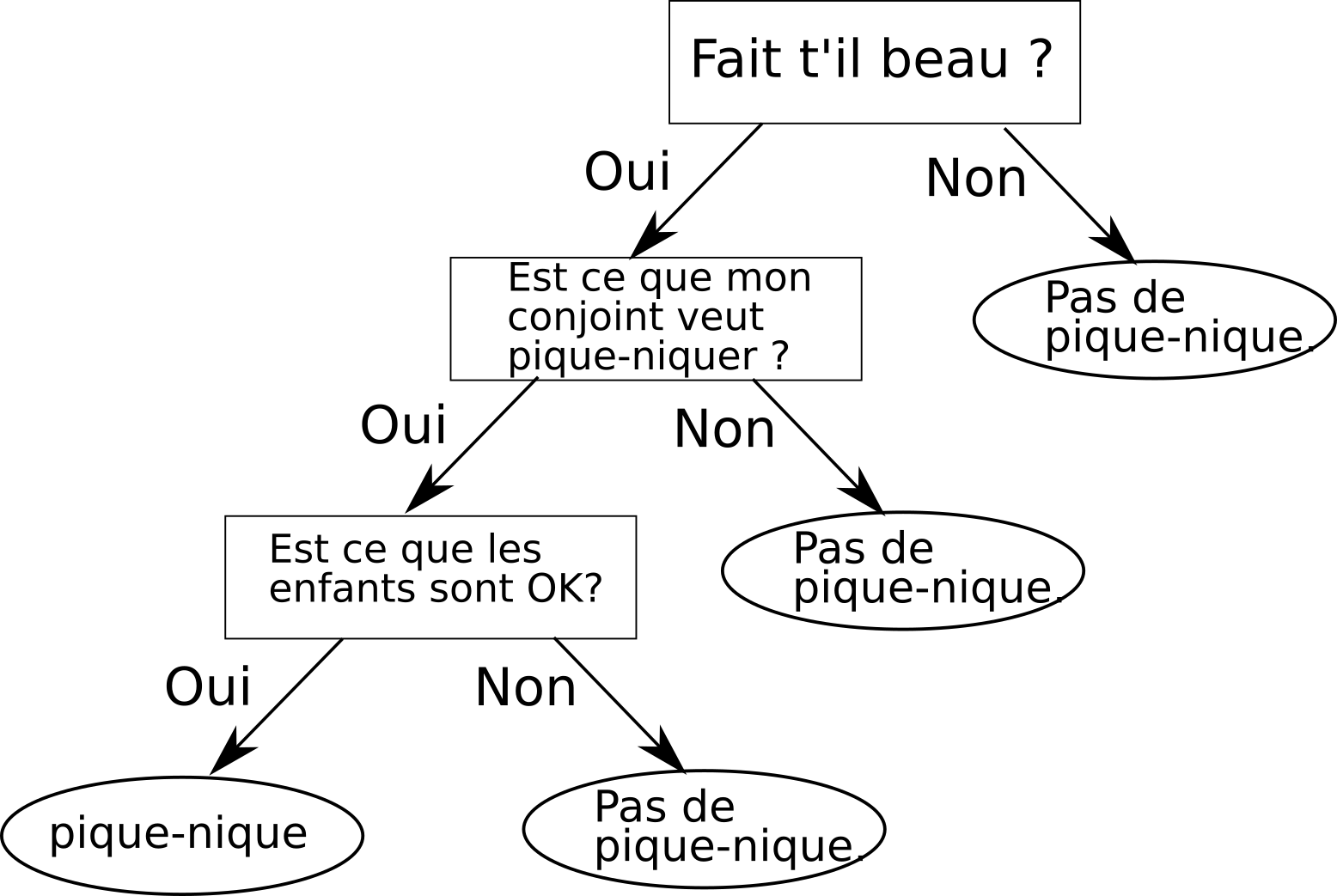
Supposons qu’aujourd’hui, vous vouliez pique-niquer avec votre compagne ou compagnon et vos enfants.
Tout d’abord pour savoir si cela est possible, vous allez d'abord vous assurer qu'il y a du beau temps aujourd'hui, car il serait bête d'aller pique-niquer et que la pluie vous tombe la dessus.
Si c'est le cas, vous allez alors demander à votre conjoint(e) si elle est intéressée à l'idée de pique-niquer. Si ça ne lui dit pas, on s'arrête la, ça ne sert à rien d'aller demander aux enfants.
Mais sinon, si ça lui dit, ben, vous irez alors demander aux enfants si eux aussi, ils sont également "OK" pour aller pique-niquer aujourd'hui.
Et si c'est le cas, vous et votre famille irez passer une agréable journée dans un parc ou sur une plage.
Le processus de décision que je viens de décrire est une bonne illustration du principe de fonctionnement d'un arbre de décision.
J'ai d'ailleurs réalisé ci-dessous l'arbre de décision correspondant à ce processus.
arbre_decision = DecisionTreeClassifier()
Une fois que le modèle a été choisi et initialisé il est temps de l'entraîner.
Avant d'entraîner le modèle, il est nécessaire de séparer la base en deux base, la base d'apprentissage et le base de test.
La raison à cela est simple, il n'est pas possible d'entrâiner un modèle sur une base et de le tester sur la même base car le fait qu'il ait été entraîner sur cette base il connaît déjà la classe de tout les exemple de cette base.
C'est pourquoi le jeu doit être séparer en une base d'apprentissage et en une base de test.
La première servira à entraîner le modèle tandis que la seconde servira à tester le modèle.
Pour ce faire, nous allons utiliser la fonction train_test_split de scikit-learn elle permet de séparer un jeu de données en un jeu d'apprentissage et un jeu de test.
#Split de la base principale en une base d'app et de test
X_train, X_test, y_train, y_test = train_test_split( iris_data, iris_classe, test_size=0.33, random_state=42)
model.fit(X_train, y_train)
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn import preprocessing
import numpy as np
import tensorflow as tf
L'entraînement du modèle se fait en appelant la fonction fit.
model.fit(X_train, y_train, epochs=500)
Elle prend principalement pour paramètre les exemples d'apprentissage, leurs classes et le nombre d'époque. Nous allons tout de suite mettre en pratique tout ce que l'on a appris avec un exemple.
#Encodage des classes afin qu'elles soit utilisable par le réseau de neurones
le = preprocessing.LabelEncoder()
#[Iris-virginica,Iris-versicolor,Iris-setosa]=>[1,2,3]
iris_classe=le.fit_transform(iris_classe)
#[1,2,3]=>[[1,0,0],[0,1,0],[0,0,1]]
iris_classe=tf.keras.utils.to_categorical(iris_classe,num_classes=3,dtype='float32')
#Split de la base principale en une base d'app et de test
X_train, X_test, y_train, y_test = train_test_split( iris_data, iris_classe, test_size=0.33, random_state=42)
#Opération centrer-réduire les données
scaler = preprocessing.StandardScaler().fit(X_train)
X_train=scaler.transform(X_train)
X_test=scaler.transform(X_test)
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import cross_val_score
#importation du dataset Iris
iris = load_iris()
#déclaration d'un arbre de décision
arbre_decision = DecisionTreeClassifier()
#calcul du score en cross-validation obtenu par l'arbre de décision sur le jeu de données Iris
scores = cross_val_score(arbre_decision, iris.data, iris.target, cv=5)
#Affichage des résultats
print ("Le score obtenu pour chacun des 5 fold créé est : ",scores)
print ("Cela fait une moyenne de : ",scores.mean())
print ("Et un écart-type de : ",scores.std())
Résultat :
Le score obtenu pour chacun des 5 fold créé est : [0.96666667 0.96666667 0.9 1. 1. ]
Cela fait une moyenne de : 0.9666666666666668
Et un écart-type de : 0.036514837167011066
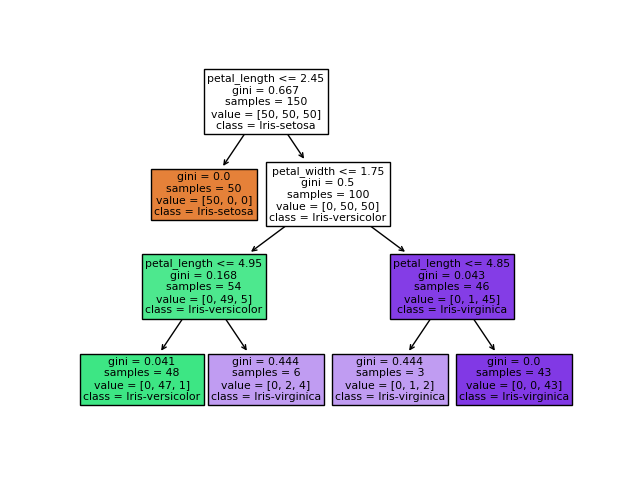
Un truc qui est cool avec les arbres de décision c'est qu'il permet d'expliquer pourquoi les décisions prisent par le classifieur sont bonnes.
Arbre de décision obtenu :
Pour évaluer un modèle, il faut utiliser ce qu'on appelle couremment en machine learning, la cross-validation ou validation croisée.
Classiquement, quand l'on entraine un modèle, l'on définit un jeu d'apprentissage sur lequelle l'on entraînera le problème, éventuellement un jeu de validation qui nous permettra de valider que le modèle est bien entraîné et de trouver les hyperparamètre optimaux du classifieur, et enfin un jeu de test qui nous permettra de nous faire une idée de la réel performance du modèle.
La cross-validation, pousse le schéma précédent un peu à l'extrême dans l'idées qu'on va le faire de nombreuse fois, idéalement 5 ou 10 fois si je jeu de données est suffisamment grand pour le permettre.
L'idée est la suivante : la cross validation consiste à scinder un jeu de données en k différents jeu de test, avec pour règle qu'aucun exemple du jeu de données initital ne peut se appartenir à deux base de test différentes. Par conséquent, nous nous retrouvons avec k base de test toute ayant k/nombre total d'exemple comme nombre d'exemple pour tester.
Le reste des exemple obtenu pour chaque base de test est utilisé comme base d'apprentissage.
Il y a plusieurs manière de faire cela avec la bibliothèque scikit-learn, mais la plus simple et rapide reste d'utiliser directement la fonction de scikit-learn prévu à cette effet :cross_val_score()
Ci-dessous, tu peux voir le prototype de la fonction
De manière générale, quand l'on test un modèle de classification, l'on parlera d'accuracy ou encore de classification rate (Taux de bonne classification), tandis que lorsque l'on est dans le cas d'un modèle de régression l'on parlera de "Mean Squarred Error" ou encore "erreur moyenne carrée" qui est simplement la moyenne du carré de la différence constatée entre la prédiction et la vraie valeur.
Comme tu peut le voir ci-dessus, cette méthode prend a 3 paramètres principaux, qui sont le modèle, la base d'exemple, la base de labels des exemples et enfin le nombre split que tu souhaite pour effectuer ta cross-validation. En sortie tu auras le taux de prédiction que la fonction a obtenu pour chacun des folds qu'elle a créé.
En clair ça donne une truc comme ça :
[accuracy_fold1, accuracy_fold 2, ...., accuracy_fold_k]
[0.9,0.8.0.7,......,0.92]
Pour avoir une idée du résultat global, il est possible d'utiliser la moyenne de ce dernier :
moyenne_accuracy=accuracy_pour_tout_les_folds.mean()
La standard déviation est également utilisée pour évaluer la stabilité du modèle d'une base app à l'autre :
std_accuracy = accuracy_pour_tout_les_folds.std()
On va illustrer tout cela avec un petit exemple avec le jeu de données Iris. Je t'explique rapidement le délire :
Le jeu de données Iris est un Jeu de données qui a été constitué à partir de mesures prélevé des fleurs appartenant à 3 espèce différentes (Iris-setosa, Iris-versicolor et Iris-virginica). Il est constitué au total de 150 exemples avec 50 exemple pour chaque espèce. Les quatre mesures qui ont été prélevées sont : la longueur de sépale, la largeur de sépale, la longueur de pétale et la largeur de pétale.
Il s'agit d'un perceprton multicouche avec 2 couches cachées de 8 neurones et entraiîner via la rétropropagation du gradient. En gros le code est le suivant :
Et le résultat :
Le score obtenu pour chacun des 5 folds créés est : [1. 0.96666667 0.96666667 0.93333333 1. ]
Cela fait une moyenne de : 0.9733333333333334
Et un écart-type de : 0.02494438257849294
On remarque qu'il est de 97.3 pour le 5 fold . Il est bien meilleurs comme pouvait me laissé pensé ma première intuition.